
今回は、機械学習でよく使われる損失関数「交差エントロピー」についての考察とメモ。
損失関数といえば二乗誤差が有名ですが、分類問題を扱う際には交差エントロピーが頻繁に使われます。
そこで、「なぜ分類問題では交差エントロピーが使われるの?」ってところが気になったので自分なりに調べてみました。
交差エントロピーの意味
まず交差エントロピーは、以下の式で表されます。
$$E=-\sum_{k}{{q(k)}log(p(k))}$$
pは、ニューラルネットワークで学習された確率。分類問題では学習データの正解率として出力されます。
qは、教師データの確率。1(100%)と0(0%)で出力されます(詳しくは後述)
ちょっと数学チックに言うと、「確率分布pと確率分布qの近似性を表現する関数」と言うことになります。
この性質から、機械学習の損失関数に交差エントロピーが採用されています。
ちなみに、「交差」というのは2つの確率分布pとqを組み合わせていることに由来しているらしい。
さらに、分類問題で使う際にはシグマのない非常にシンプルな数式になります。
$$E=-log(p(k))$$
分類問題の場合、教師データは全て0と1になります。つまり0%か100%かという二択になるということ。
例えば、とある画像群から「あ」「い」「う」「え」「お」の文字を学習させる時、教師データは[0,0,0,0,1]のような形で与えられ、
[1,0,0,0,0]は「あ」
[0,1,0,0,0]は「い」
[0,0,1,0,0]は「う」
[0,0,0,1,0]は「え」
[0,0,0,0,1]は「お」
・・・といった感じで教師データを作ります。(one-hot表現というやつ)
なので、シグマで合計値をとっても、教師データは正解データ(1のデータ)以外は全て0となり、残るのは正解データの一項のみとなるわけです。
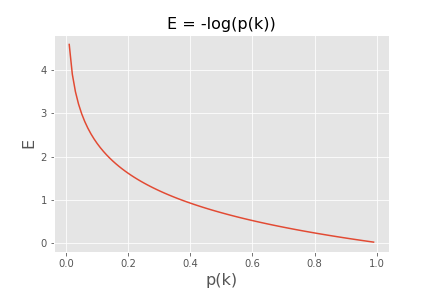
グラフにするとこんな感じ。p(k)は学習データが教師データと同じになる確率を表現しているので、0<p(k)<1。一般的な対数関数です。
p(k)が小さいということは教師データが1(100%)なのに、学習結果が0.1(10%)となっているようなケース。教師データと学習結果が乖離していればしているほど、数値が大きくなる(p(k)が小さいとE(損失関数)の値が大きくなる)。まさに損失関数そのものです。
二乗誤差関数と交差エントロピーの違い
損失関数として使われる二乗誤差関数と交差エントロピー。この2つの違いは何かと言うと、
という点です。
学習の速さは損失関数の微分値の大小に依存しています。というわけで、二乗誤差関数と交差エントロピーの微分値を比較してみました。
二乗誤差関数はこんな数式。回帰分析などでよく使われます。
$$-\frac{1}{2}\sum_{k}{(y_k-t_k)^2}$$
yは、ニューラルネットワークの出力結果。
tは、教師データ。
kはデータの次元数です。上の例で、「あ、い、う、え、お」は[0,0,0,0,1]といった5つのデータで表現しているのでk=5となります。
さて、この二乗誤差関数をyで微分するとこんな数式になります。
$$\sum_{k}{(-y_k+t_k)}$$
yの一次関数です。
一方の交差エントロピーは微分するとこんな数式になります。
$$-\sum_{k}\frac{t_k}{y_k}$$
yは、ニューラルネットワークの出力結果。
kはデータの次元数です。前述したように、交差エントロピーは教師データが0の項は全て0になるので、実際はシグマが外れてもっとシンプルな式になります。
$$-\frac{1}{y_k}$$
整理すると・・・
さらに2つのグラフを1つにするとこんな感じ。(今回は分類問題を考えているのでyの範囲は0〜1に限定しています)
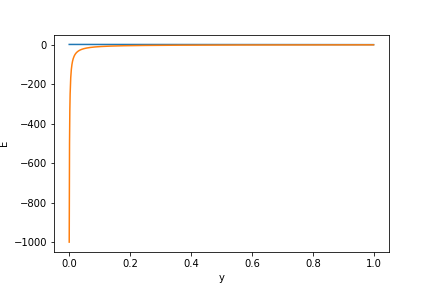
青線が二乗誤差。黄線が交差エントロピーの微分値です。
出力結果(y)が0に近いところだと、交差エントロピーの微分値がとてつもなく大きなマイナスになっていることがわかります。微分値が大きなマイナスになっているということは、それだけ損失関数がマイナスに大きく変動しているということを意味しています。
交差エントロピーは、出力結果(y)が0に近ければ近いほど教師データとの誤差が大きいわけなので、誤差が大きい時(yが0に近い)ほど微分値が大きい、つまり損失関数の変動が大きいということになります。(損失関数の変動が大きい=学習効率が良い!)
まとめると、
ということが言えるわけです。
これはあくまで分類問題の話であり、「出力結果が0付近で学習速度がUPする」という性質なので、回帰分析などに応用する時は注意が必要かもしれません。
一般的に「分類問題の損失関数は交差エントロピーを使う」と言われていますが、学習の速さが違うだけで理論上は二乗誤差関数を損失関数にしても分類問題を扱うことも可能なはず。(非効率ですし、あえて使う人は少ないかもしれませんが)
「なぜ分類問題には交差エントロピーを使うのか?」疑問に思ったので、調べたことを記事としてまとめてみました。分類問題の場合は、迷ったりわからなくなったりしたら、とりあえず交差エントロピーを損失関数に使っておけば間違いはないということがわかりました。



コメント
ディープラーニングの勉強をしていますが、
分かりやすくてすごく良かったです。
交差エントロピー誤差を何に利用するのか具体的にイメージできました。
良い記事だと思いました。
理由が理解できてスッキリしました。