
今回は、株価を使って分散・標準偏差について知りましょう!って話です。
投資の世界では分散・標準偏差はとても身近な存在です。投資の話でよく耳にするボラティリティなんかは、標準偏差そのものです。
と言うわけで、株価データを使って分散について色々見ていきます。
分散・標準偏差とはデータのばらつき具合のこと
まず、「分散・標準偏差とはなんぞや?」って話ですが、簡単に言うとデータのばらつき具合を示す指標です。
正規分布をする事象を考えます。株価で言うと株価の日々の変動率が正規分布に似た形をします。(分足・時足とかでも同じ)
例としてソニー(6758)の株価を見てみます。下の図は、2007年1月5日〜2019年2月28日までの計2965日分の株価の変動率をまとめたヒストグラム。変動率は前日終値と当日終値の変動率を使いました。(ニュースなどで一般的に使われる変動率です)
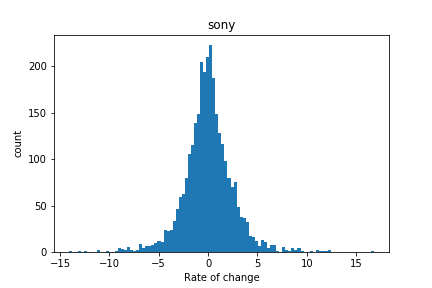
日々の変動率の平均値は0.0317%となっています。山なりになっているヒストグラムの頂点付近が平均値になります。
そして分散・標準偏差というのは、平均値から離れたデータがどれぐらいあるかを示す指標として使われます。
標準偏差の話は後にするとして、まず分散について紹介すると、分散は以下の数式により計算されます。
$$s^2=\frac{1}{n}\sum_{k=1}^{n} {(x_i-μ)^2}$$
平均値と個々の数値の差を二乗した値を全て足し、最後にデータの数nで割った値が分散です。
ソニーの株価変動率の分散を求めてみると、6.167になりました。
・・・が、これだけでは分散は使えません。分散が威力を発揮するのは次の2つのケースです。
分散値そのものに意味はない
上の例で計算したソニーの分散値である6.167。実はこの数値自体に意味はないんです。
この数値が意味を持つには、「他の銘柄の分散値と比べて大きいか小さいか」という比較をする必要があります。
ここでもう1つ、比較対象としてファナック(6954)の分散値を計算してみます。

平均値と分散値を計算してやると
平均値:0.0430
分散値:5.581
です。ここで初めて「ソニーとファナックの分散値を比べると、ソニーの方が分散値が大きい。つまり、ソニーの方が値動きが大きい」という風に分散を使うことができるようになります。
株式投資の場合、分散値の大きさはそのままリスクに関係してきます。
分散と標準偏差の違い
次に分散と標準偏差の違いについて話しておきます。
$$s^2=\frac{1}{n}\sum_{k=1}^{n} {(x_i-μ)^2}$$
$$s=\sqrt{\frac{1}{n}\sum_{k=1}^{n} {(x_i-μ)^2}}$$
上の式の通り、分散と標準偏差には「標準偏差の二乗が分散」という関係があります。株式投資の世界では、分散よりも標準偏差を用いるケースが多いです。
その理由は次に説明する「正規分布」に隠されています。
正規分布における標準偏差はとっても便利!
実は、正規分布をする事象に標準偏差を使ってやるととても面白いことがわかります。正規分布上では、事象が標準偏差(±s)内に収まる確率は68%だということがわかっているんです。
例えば、上での例で使ったソニーとファナック。この2銘柄の分散と標準偏差を計算するとこんな感じになります。
| 分散(s^2) | 標準偏差(s) | |
| ソニー | 6.167 | 2.483 |
| ファナック | 5.581 | 2.362 |
そして、ソニーもファナックも株価の変動率が正規分布に従うと仮定すると、
ソニーの株価の値動きは68%の確率で±2.483%以内に収まり、ファナックの株価の値動きは68%の確率で±2.362%以内に収まる・・・ということがわかるのです。
±s内に収まる確率は68%ですが、話には続きがあって、
±2s内に収まる確率が95%
±3s内に収まる確率が99.7%
であることもわかっています。ソニーとファナックについて計算してやると
| 68%以内(±s) | 95%以内(±2s) | 99.7%以内(±3s) | |
| ソニー | -2.483〜+2.483 | -4.966〜+4.966 | -7.449〜+7.449 |
| ファナック | -2.362〜+2.362 | -4.724〜+4.724 | -7.086〜+7.086 |
という結果になります。
気づいた人もいるかもしれませんが、これはテクニカル指標で使われているボリンジャーバンドそのものです。(厳密には不偏標準偏差と標準偏差の違いがある)
しかし、実際の株価の値動きは正規分布通りにはなりません。試しにファナックの2695日間の実際値動きと上の68%、95%、99.7%に収まる確率を比較してみます。
| 値動き幅 | 正規分布 | 実際の値動きの確率 |
| -2.362〜+2.362 | 68% | 76.9% |
| -4.724〜+4.724 | 95% | 95.8% |
| -7.086〜+7.086 | 99.7% | 98.6% |
という結果になりました。ファナックの値動きは、
ということがわかります。

図で表現すると
ということです。68%、95%、99.7%の話をまとめると以下のイメージ。
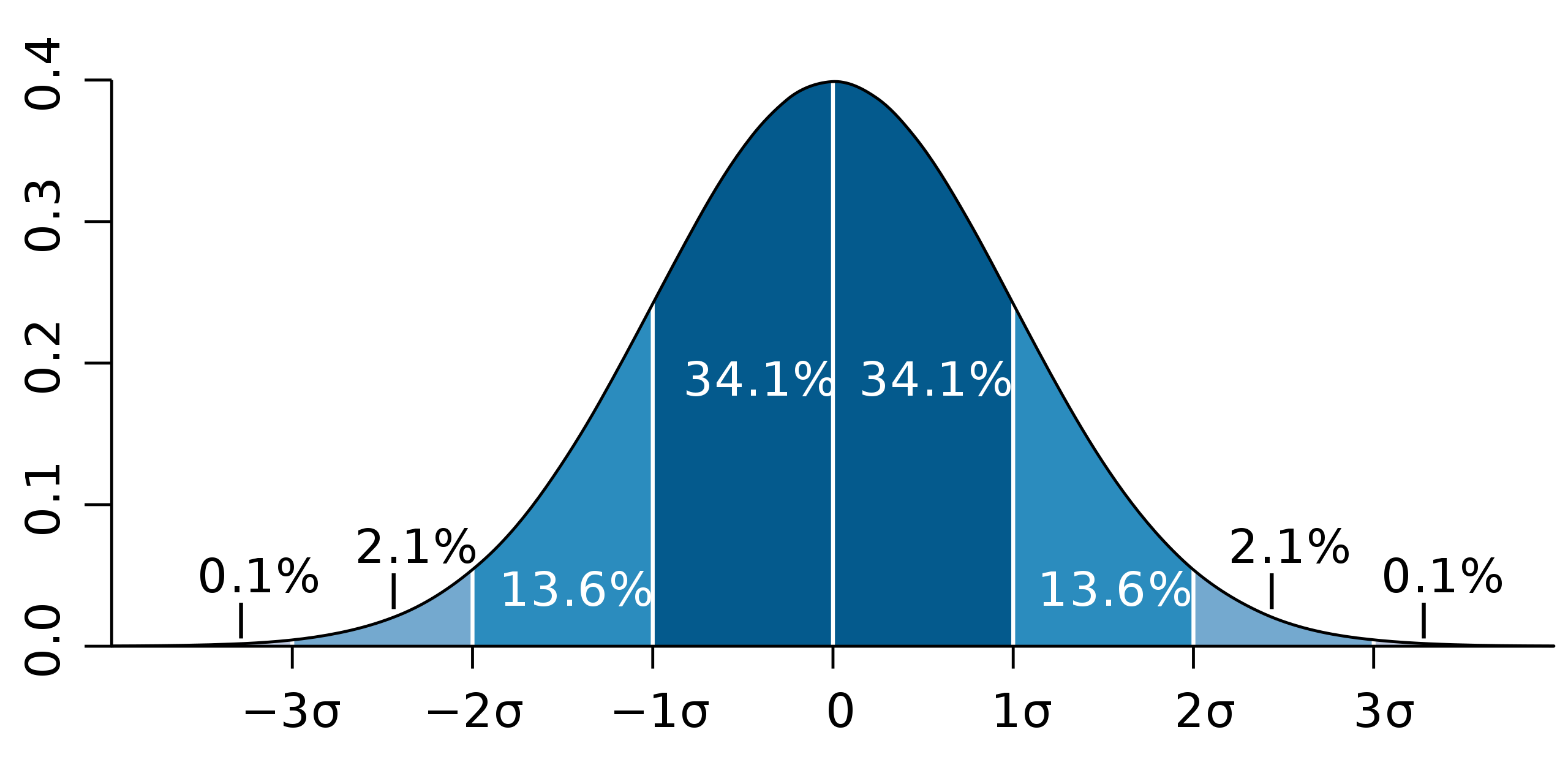
(出典:wikipedia「標準偏差」)
今回は分散・標準偏差のお話をしましたが、もう1つ似た言葉として不偏分散・不偏標準偏差って言葉もあります。
不偏標準偏差は株価の世界でいうボラティリティと同じ意味です。知っておいて損のないお話だと思います。以下の記事で整理していますので、合わせてどうぞ。




コメント