
今回は、統計における相関性について株価データを使って色々と考察してみようと思います。
株価でいう相関性とは例えば、トヨタ(7203)、コマツ(6301)、NTTドコモ(9501)、KDDI(9613)の4つの株価データを見る時に、
とか複数の銘柄の値動きを関係付けて考える時に使える統計手法です。
相関性については、私自身勉強不足のため誤っている部分があるかもしれません。何かあればご連絡いただけると嬉しいです。
相関性の公式を確認しておく
相関性は、相関係数という数値によって知ることができます。
相関係数はpython,R,エクセルなどで簡単に計算できるため実際に数式を見る機会は少ないですが、一応ここで掲載しておきます。
$$r=\frac{s_{xy}}{{s_x}{s_y}}$$
s_xとs_yは比較したい2つの対象の標準偏差
$$s_x=\sqrt{\frac{1}{n}\sum_{k=1}^{n} {(x_i-μ)^2}}$$
$$s_y=\sqrt{\frac{1}{n}\sum_{k=1}^{n} {(y_i-μ)^2}}$$
s_xyは共分散と呼ばれる式。
$$s_{xy}=\frac{1}{n}\sum_{k=1}^{n} {(x_i-μ)(y_i-μ)}$$
複雑な数式ですが、実際に算出するときはプログラムで一瞬で計算できるので、覚える必要はないです。
計算される数値は−1から1の範囲内に収まり、一般的に以下のような相関性を示します。
| 相関係数(r) | 相関性 |
| -1 ~ -0.7 | 強い負の相関 |
| −0.7 ~ -0.4 | かなりの負の相関 |
| −0.4 ~ -0.2 | やや負の相関 |
| −0.2 ~ 0.2 | ほとんど相関なし |
| 0.2 ~ 0.4 | やや正の相関 |
| 0.4 ~ 0.7 | かなりの正の相関 |
| 0.7 = 1 | 強い正の相関 |
ここで、登場する「負の相関性」「正の相関性」とは
ってことです。
「百聞は一見に如かず」というわけで、株価のデータを使って実際に相関性を考察してみます。
株価の相関性を見てみる
サンプルとして、トヨタ(7203)、コマツ(6301)、NTTドコモ(9501)、KDDI(9613)のデータを使って相関性を見ていきます。
4銘柄の計2695日分の前日終値と当日終値の価格変動率を使います。
pythonのpandasデータフレームを使うと相関係数は一瞬で計算することができます。pythonのコードはこんな感じ。dfデータフレームに4銘柄の変動率を入れてcorrメソッドを実行するだけ。
df.corr()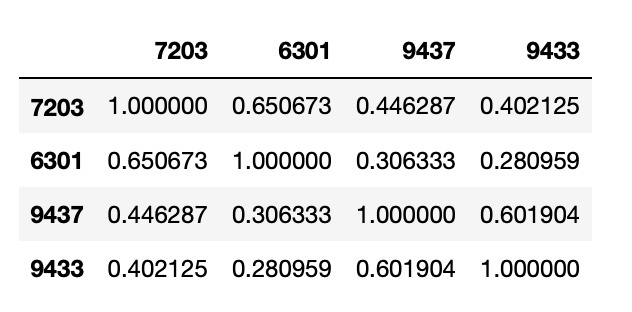
df.corrは、相関係数を上記のような行列形式で表示します。行列形式にすると全ての相関係数を一気に見ることができて便利。
視覚的にもっとわかりやすくするため、ヒートマップにしてみます。(コードを載せてますが、その説明は省略します)
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
sns.heatmap(df.corr())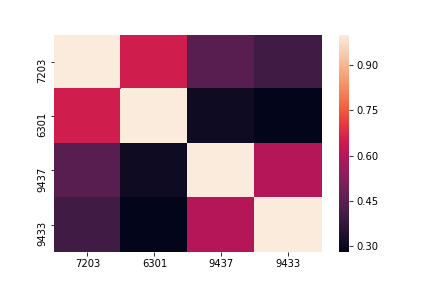
ヒートマップにするととても見やすいです。黒っぽくなればなるほど相関性が低くなっていきます。
このヒートマップを見ると以下のことがわかります。
この4つ銘柄だけに限るなら、景気敏感株とディフェンシブ株の値動きには相関性は少ないということが言えそうです。
相関係数の信用度を確認するp値
ところで、上で計算した相関係数はどこまで信用できる数字なんでしょうか。
本当は相関性がないのに、私の使ったデータ(2007年〜2019年の株価データ)だけたまたま相関性があるように見えるだけかもしれません。
これを確認するための値としてp値というのが用いられます。小難しい話を全部省略するとp値は、
「相関性が0と仮定した時に、偶然に0.4とか0.6とかの相関係数が出てしまう確率」を意味します。
上の例だと一番大きかったトヨタ・コマツの相関係数は0.65です。この時、もしp値が0.3だとすれば、相関性が0でも30%の確率で0.65の相関係数がでるということ意味しています。
つまり、0.65で一見正の相関性がありそうでも、30%の確率で相関性が0ということになります。これじゃあ0.65の数値を安易に信じることができなくなります。
そこで、相関係数を計算したら、その後p値を求めることが一般的です。p値が0に近ければ近いほど、「相関性が0だけど運悪く強い相関性が計算されてしまう確率」が低くなるので数値の信用度が上がっていきます。
上の4銘柄は共にp値は0.001以下であり、数値の信頼性はありそうです。(もしかすると、「見せかけの回帰」に関連してもう少ししっかり考察する必要があるかもしれない。)
株価データの分布図で相関性を見てみる
もう1つ、相関性を視覚的に確認する方法として分布図を使うことが良くあります。
相関係数の一番大きかったトヨタ・コマツ、と一番小さかったコマツ・KDDIの分布図を実際に見てみましょう。

まずはトヨタとコマツから。
正の相関性が強い場合はプロットされた点は右肩上がりになり、負の相関性が強いと右肩下がりになります。(これは正負の相関性の定義からわかります。)
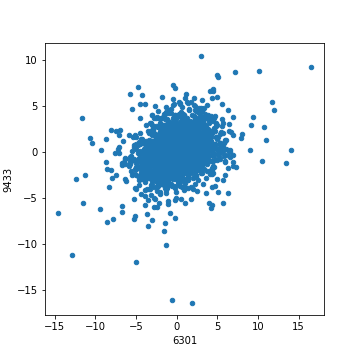
次にコマツとKDDI。相関性が小さい場合の分布図です。
相関性が小さい場合、プロットされた点は右肩上がりにも右肩下がりにもならず、ぼんやりと円を描くように乱雑な形になります。(上の場合、円を描きつつも相関係数がプラスなので気持ち右肩上がりになっている)
pythonの場合以下の、コードで散布図を行列表示することができます。
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
sns.pairplot(ratio_df, size=2.5)
plt.show()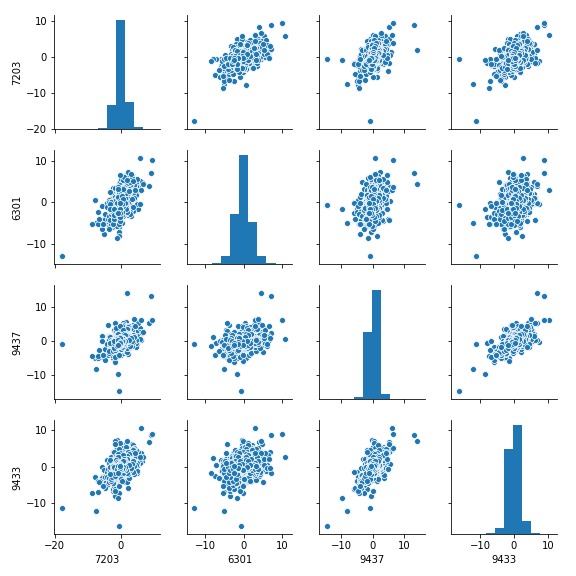
(この散布図行列のデータは、上のデータとは異なるデータ個数で出力しているため上の図とは形状が違いますのでご注意を)
個別株では負の相関性は見つけずらい
さてこれまでの相関性の話をリスク管理の話に置き換えると次のことが言えそうです。
実際はこんな単純な話ではありませんが、傾向の1つとしては正しく思えます。
しかしながら、この記事を書きながらいろんな銘柄の相関性を見て感じたのは、日本株の個別銘柄同士で強い負の相関性を持つケースはかなりレアなんじゃないか・・・?ということ。
私の場合は日経225銘柄のみで考察しているため、「日経225に組み込まれている時点で全ての銘柄は正の相関性が出やすい傾向がある」ってことなのかもしれません。また、負の相関性は、株と国債、株とゴールドみたいにもっと大きな視点で投資対象を比較する必要があるようにも思います。
負の相関性を持つ銘柄が少ないとすれば、個別株でリスク管理をする方法は、正の相関性が強い銘柄を見つけて、売りと買いの逆トレードをするという手法を採用するのが良いのかもしれません。
余談ですが、日経平均と先物の相関性を見ると超強い正の相関性になっているはずです。(私は先物のデータを持っていないのここで示すことはできませんが・・・)そして、この強い正の相関性を使って、ヘッジファンドは先物売りand現物買いの逆トレード(いわゆる裁定買い)をすることで、リスク管理をしています。



コメント